蠱惑の楽器たち 117．倍音の基本

音楽における倍音の重要性

音楽のあらゆる要素は倍音の影響を受けていますので、倍音のことが分かると様々な応用が可能になります。音色、音律、スケール、コードなどは、全て倍音が基本となっています。しかし、音楽分野では倍音から派生した理論については追及しますが、倍音そのものは科学的すぎるためか、あまり本格的に扱うことはないと思います。ここではあえて物理的な側面から掘り下げてみたいと思います。

以下リンクは倍音関係の過去記事となります。さわり程度の内容ですが参考まで。

• 10．楽器の音色（倍音１）
• 11．楽器の音色（倍音２）
• 15．楽器の音律

倍音とは？

音程がある楽器音は主に倍音とノイズで作られています。ギターなどで何気なく弾いた音にも多くの倍音が含まれています。倍音ひとつひとつは周波数の異なるサイン波であり、周波数は整数比となっています。サイン波は倍音を持たない音で、正弦波、純音とも呼ばれます。

上記波形をサイン波に分解すると、以下のように4個のサイン波になります。ちなみに基音（1）、2倍音、3倍音、5倍音で構成されていて、周波数は基音x倍音となっています。視覚的にも倍音が整数比となっているのが確認できると思います。

音程感のある楽器が整数比の倍音で構成されている理由

次に生楽器も見てみます。まずはギターの5弦開放の音A2（110Hz）の音を鳴らしてみます。

この音をリニア表示の周波数スペクトルで見てみます。針のようなピークとなっている音が倍音で、その周波数は整数比です。そのレベルの違いや、変化、ノイズとの関わりでサウンドが決定され、ギターらしい音となります。これを見ると、アタック後はすぐに倍音が消えて、リリース中は、少ない倍音で構成されているという印象です。

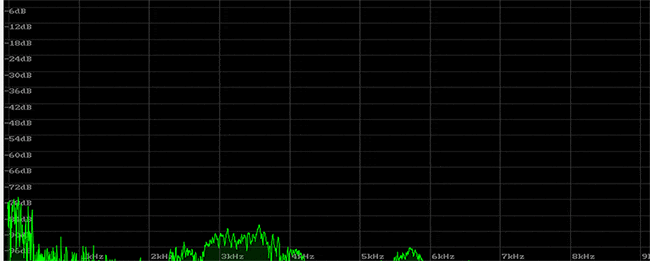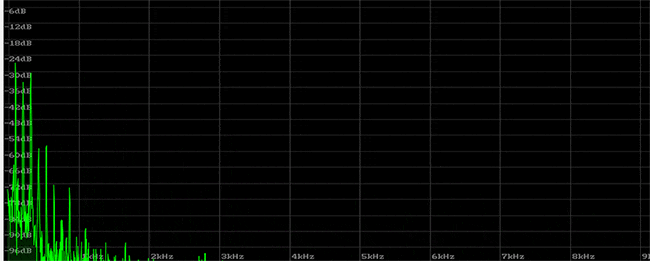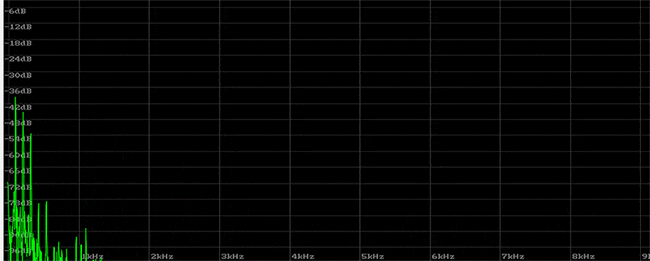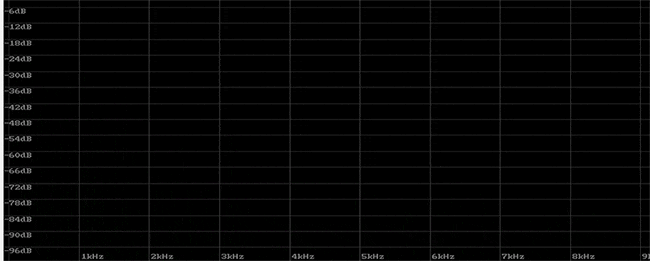
では、なぜピークの倍音が整数比になるのでしょうか？まずギターを使って倍音だけを鳴らしてみます。ギターは倍音だけを鳴らすナチュラル・ハーモニクスという奏法があり、2、3、4、5、6倍音と順次鳴らしてみます。この奏法を使った音は、倍音が少なく、サイン波に近い音になります。はじめの音だけは開放弦を普通に弾いています。

上記の音を物理学的に図にすると以下のような振動となります。これは鳴っているギター弦をよく観察しても感じ取れる現象です。交点にあたる部分がハーモニクスポイントとなっていて、ここに指を軽く触れて弾くと得られるというわけです。鳴っている時に、この交点に指で軽く触れる程度では音は止まりません。逆に盛り上がっている箇所に触れると、明らかな振動を感じ音は減衰します。

• 基音=1は、弦全体の長さで振動していて、一番低い音です。上記のサンプルでA2（110Hz）が鳴っています。
• 2倍音は、半分の長さが振動しています。つまり1オクターブ上の音であり、A3（220Hz）となります。
• 3倍音は、1/3の長さの振動となり、110Hz x 3 = 330Hz、つまりE4となります。
• 4倍音は、1/4の長さの振動でA2の2オクターブ上のA4（440Hz）となります。
• 5倍音は、1/5の長さの振動となり、110Hz x 5 = 550Hzとなります。平均律ではC#5（554Hz）に近いですが、若干低い音となります。
• 6倍音は、1/6の長さの振動となり、110Hz x 6 = 660Hzとなり、E5となります。3倍音のオクターブ上です。

また、どの倍音も必ず基音を等間隔で分割しています。逆に等間隔に分割できない音は、物理的に振動しにくいわけです。実際にハーモニックポイント以外では、きれいに伸びる音を鳴らすことはできません。以上が整数比の倍音で構成される理由となります。特に弦楽器や管楽器が顕著と言えます。

倍音の間隔について

倍音の出方次第でサウンドが決定され、各楽器のサウンドの違いは倍音の出方が大きな要因となります。倍音を並べて、振幅を倍音で割るとノコギリ波となります。奇数倍音を並べて振幅を調整すると矩形波となります。このように一定のルールで倍音を並べることで幾何学的かつ理想的な基本波形を作ることができます。また非整数倍音が含まれると金属的な音になったり、音程感がなくなる方向になります。

次に電子的に32倍音まで使ってノコギリ波を作ってみます。理想的なノコギリ波は倍音をすべて含むため、実験等で扱いやすい波形です。倍音が多いほど理想的なノコギリ波に近づきますが、ここでは説明用に32倍音までとしました。リニア表示の周波数スペクトルで表示すると、各倍音のレベルと、等間隔であることが確認できます。人間の感覚ではオクターブの関係が等間隔に感じるため、対数表示にすることが多いですが、倍音に関してはリニア表示の方が直感的になります。

上記を音にすると以下のようになります。ノコギリ波としては倍音が少なめのサウンドです。

さらにC3（130.8Hz）の基音から32倍音のC8（4186Hz）まで、倍音だけを順次鳴らしてみます。

この32倍音までを鍵盤に対応させると以下のようになります。多くの場合、低次倍音ほど強く出る傾向にあり、重要な音となります。20倍音を超えると、半音以下のステップとなり、12平均律に慣れている現代人からすると、かなり違和感のある音となります。それでも同時に鳴ると全く気にならなくなり、ノコギリ波として整然と響くところが不思議ではあります。

さらにサークルで表現すると平均律との差が分かりやすくなります。オクターブを12等分したものが平均律で基準線を引いておきました。そこに螺旋状に32倍音までプロットしています。低次倍音は飛び飛びですが、高次倍音になるほど間隔が狭くなっていき、半音以下になります。自然な音の多くは、高次倍音ほど減衰するため、重要性は薄れて行きます。

各倍音を見ると基音及び2倍音（I）は基準なので平均律とピッタリです。5度（V）、2度（II）は、平均律にかなり近い位置にあり、誤差の範囲と言えます。短2度と短3度も誤差の範囲と言えますが、倍音としては17倍音、19倍音と距離があり、関係性としては遠のきます。それ以外は平均律からは、それなりにズレています。響きを重視したい場合は、倍音に素直であるべきですが、現在の音楽のほとんどは平均律で作られており、濁りが生じてしまう理由はここにあります。またブルースや民族音楽では、部分的に平均律よりも、倍音に近い音程を好む傾向にあり、それがそのジャンルの特徴のひとつになっています。

倍音の出現順序と素数

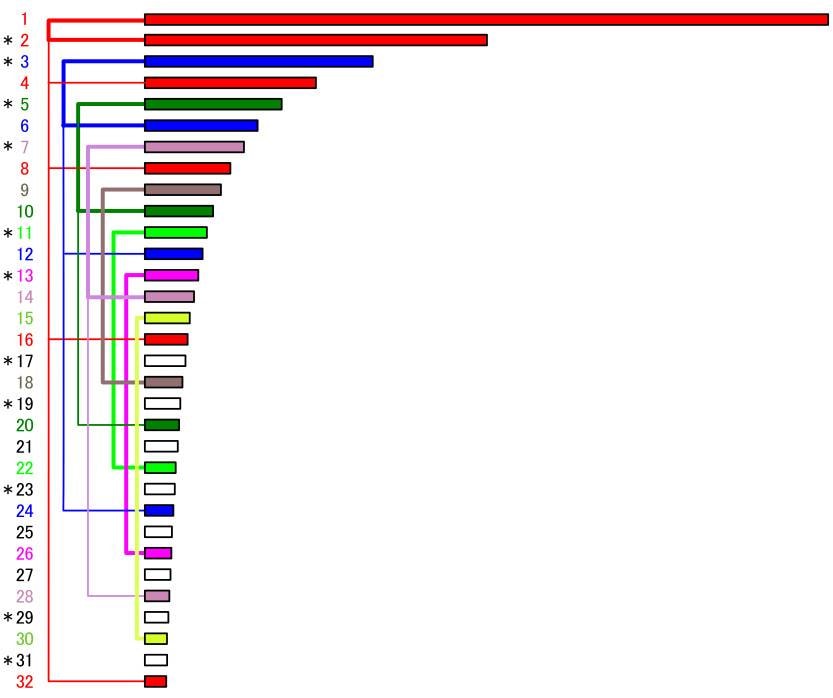
上記と違った図にすると、別の気付きがあるかもしれないので下図を用意してみました。（*印は素数です。）数値は倍音で、棒の長さは各倍音の周期となります。倍音は数学的には整数比できれいに並んでいますが、音楽的な視点で見ると、共通している音と、そうでない音という分類ができます。基本的にはオクターブ違いの音は同一視することが多いと思いますので、色分けしています。まず初めの方に出現した音ほど頻繁に出現することになりますので、より支配的になります。32倍音中、基音=6回、完全5度=4回、長3度=3回という感じで、出現頻度はレギュラー級と言えます。これらはメジャーコードの主要3和音でもあります。次に来るのが短7度を少し低くした音です。これは意外に感じるかもしれませんが、ブルースなどでは7thコードが基本となっていることは無関係ではないと思います。また比較的素数を中心として、新しい音が出現しています。素数以外で新しい倍音としては、9倍音、15倍音、21倍音、27倍音などがありますが、これらは3倍音x3=9倍音、5倍音x3=15倍音、7倍音x3=21倍音、9倍音x3=27倍音と解釈できます。つまり既に存在している音の完全5度上という関係です。基音に対して5度の音はオクターブの次に親和性が高く、色付けをあまりしない補完的な意味合いのある音です。そのことから特定の音の3倍音=完全5度上というのは、強い関係があることを意味します。また25倍音は、5倍音x5の関係、長3度となり、5度の次に親和性があります。倍音から見ても素数は明らかに特別な数で、根源的な原理に直結しています。

次回は、倍音と和音の関係について解説します。

コラム「sound＆person」は、皆様からの投稿によって成り立っています。
投稿についての詳細はこちら