Enchanting Instruments 117 - Fundamentals of Harmonics

The Importance of Harmonics in Music

Every element of music is influenced by harmonics, and understanding them opens the door to a wide range of applications. Timbre, tuning systems, scales, and chords are all fundamentally rooted in the overtone series.
However, in the field of music, while many theories derived from overtones are explored in depth, overtones themselves are often not treated thoroughly, possibly because they are considered to be too scientific or technical.
In this article, I would like to intentionally dig into the physical (scientific) aspects of overtones.

Below are links to previous articles related to overtones. They only cover the basics, but these articles may still serve as useful references:

• 10 - Timbre of Instruments (Harmonics 1)
• 11 - Timbre of Instruments (Harmonics 2)
• 15 - Musical Tuning Systems

What Are Harmonics (Overtones)?

Musical sounds with a definite pitch—like those produced by instruments—are primarily made up of overtones and noise. Even a casually played note on a guitar contains a rich array of overtones.
Each harmonic is essentially a sine wave (a pure tone) with a different frequency, and these frequencies follow integer ratios. A sine wave is a sound without any overtones is also referred to as a pure tone or simple waveform.

When you break down a waveform (like a guitar note) into its component sine waves, you’ll find something like the example below:
The waveform consists of:
- Fundamental (1st harmonic)
- 2nd harmonic
- 3rd harmonic
- 5th harmonic
Each overtone has a frequency that is a multiple of the fundamental (e.g., 2×, 3×, 5× the base frequency).
Visually, you can also observe that these overtones follow clear integer ratios, which is a key aspect of how harmonic content shapes the character (timbre) of a sound.

Why are pitched instruments made up of harmonics in integer ratios?

Let’s take a look at acoustic instruments. First, we’ll play the open 5th string (A2, 110 Hz) on a guitar.

When this sound is viewed using a linear frequency spectrum, we can see sharp peaks form. These are the harmonics and their frequencies are in integer ratios. The differences in their levels, how they change, and how they relate to noise determine the sound, creating what we recognize as a guitar tone. Looking at this, it appears that the harmonics fade quickly after the initial attack, and during the release phase, the sound consists of fewer harmonics.

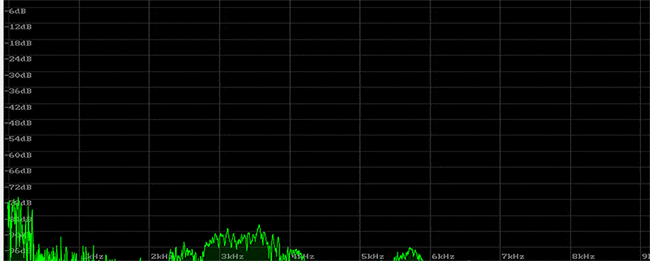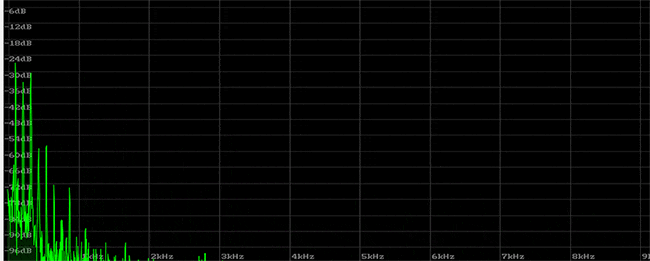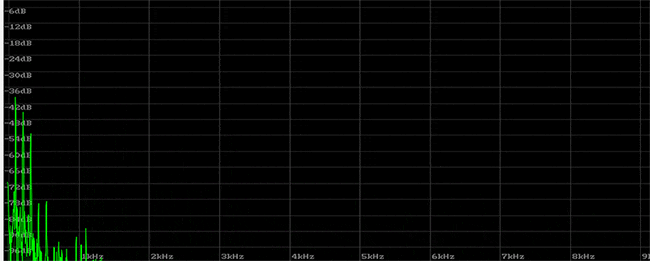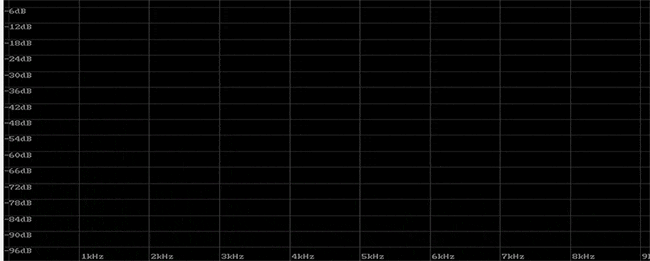
So, why do the harmonic peaks occur at integer ratios? First, let’s try playing only the harmonics on a guitar. The guitar has a technique called natural harmonics, which allows you to isolate and play only the harmonics—specifically the 2nd, 3rd, 4th, 5th, and 6th harmonics, in succession. These notes that are produced by using this technique contain fewer harmonics and sound closer to a sine wave. The first note is played normally on the open string.

Looking at this visual from a physics perspective, the vibrations of the string look like the diagram below. This is a phenomenon you can actually observe when watching a vibrating guitar string. The crossing points correspond to the harmonic nodes. When you lightly touch these points with your finger and pluck the string, the harmonic is produced. If you lightly touch one of these crossing points while the string is vibrating, the sound won’t stop. On the other hand, if you touch one of the raised areas instead, you’ll feel a distinct vibration, and the sound will quickly decay.

• 1st harmonic (fundamental) – Full string vibrates. Note: A2 (110 Hz). Lowest pitch.
• 2nd harmonic – Half the string length vibrates. Note: A3 (220 Hz). One octave above fundamental.
• 3rd harmonic – One-third of the string vibrates. Frequency: 110 Hz × 3 = 330 Hz. Note: E4.
• 4th harmonic – One-fourth of the string vibrates. Frequency: 110 Hz × 4 = 440 Hz. Note: A4 (two octaves above fundamental).
• 5th harmonic – One-fifth of the string vibrates. Frequency: 110 Hz × 5 = 550 Hz. Closest note: C#5 (554 Hz in equal temperament). Slightly flat compared to C#5.
• 6th harmonic – One-sixth of the string vibrates. Frequency: 110 Hz × 6 = 660 Hz. Note: E5 (one octave above the 3rd harmonic).

Also, each harmonic always divides the fundamental frequency into equal segments. Conversely, frequencies that do not divide the string evenly are physically harder to sustain as vibrations. In practice, notes played outside of harmonic points do not produce clear, sustained tones. This is the reason why harmonics are based on integer ratios. This principle is especially prominent in string and wind instruments.

About the spacing of harmonics

The way harmonics appear determines the sound, and differences in how harmonics are produced are a major factor in the distinct sound of each instrument. When harmonics align and their amplitudes are divided by the harmonic number, a sawtooth wave is formed. If only odd-numbered harmonics are used and the amplitudes are adjusted, a square wave results. In this way, arranging harmonics according to specific rules can produce geometric and ideal fundamental waveforms. Conversely, when non-integer harmonics are included, the sound becomes more metallic or loses a clear sense of pitch.

Next, let’s create a sawtooth wave electronically using up to the 32nd harmonic. An ideal sawtooth wave contains all harmonics, making it a waveform that is easy to handle in experiments. The more harmonics included, the closer the wave gets to an ideal sawtooth wave, but for explanation purposes, I limited it to the 32nd harmonic here. When displayed on a linear frequency spectrum, you can see the levels of each harmonic as well as the fact that they are evenly spaced. Human ears tend to perceive octaves as evenly spaced, so logarithmic scales are often used and linear displays are more intuitive when it comes to harmonics.

When the above waveform is converted to sound, it produces a tone with relatively few harmonics for a sawtooth wave.

Next, starting from the fundamental note C3 (130.8 Hz), the harmonics are played sequentially up to the 32nd harmonic, C8 (4186 Hz).

When these 32 harmonics are mapped onto a keyboard, it looks like this. In most cases, the lower-order harmonics tend to be stronger and are the most important sounds. Beyond the 20th harmonic, the intervals become smaller than a semitone, which can sound quite unusual to modern listeners accustomed to the 12-tone equal temperament system. However, when played all at once, this dissonance is hardly noticeable, and the sound resonates in order as a sawtooth wave, which is quite fascinating.

Representing this on a circle makes it easier to understand the difference from equal temperament. The equal temperament system divides an octave into 12 equal parts, and this is shown as a baseline. The 32 harmonics are then plotted spirally around this baseline. The lower-order harmonics are spaced further apart, but as the harmonic number increases, the intervals become narrower, eventually falling below a semitone. Since higher-order harmonics typically diminish in amplitude in natural sounds, their importance gradually lessens.

Looking at each harmonic, the fundamental tone and the second harmonic (octave) perfectly match the equal temperament since they serve as the reference points. The perfect fifth (5th) and major second (2nd) are also quite close to being equal in temperament, falling within an acceptable margin of error. The minor second and minor third intervals are similar within this margin, but as harmonics, specifically the 17th and 19th harmonics, they are more distant and less related. Other harmonics show noticeable deviations from equal temperament. When prioritizing pure resonance, tuning should align more naturally with the harmonics. However, most contemporary music is based on equal temperament, which is why some dissonance occurs. Additionally, in blues and folk music, there is a tendency to favor intervals closer to the natural harmonics rather than strict equal temperament, which contributes to the distinctive character of those genres.

Order of Harmonic Appearance and Prime Numbers

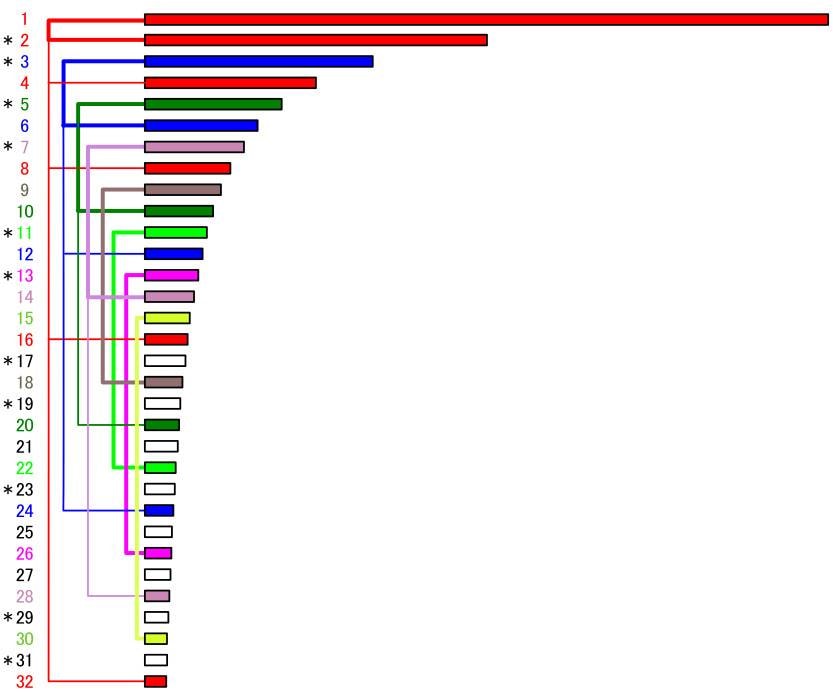
I created the diagram below to offer a different perspective from the one above.
(Asterisks mark prime numbers.) The numbers represent the harmonics, and the length of each bar shows the period of each harmonic. While harmonics are mathematically arranged in neat integer ratios, from a musical viewpoint, they can be classified into notes that are commonly shared and those that are not. Octave-related notes are usually considered the same, so I color-coded them accordingly.
Harmonics that appear earlier tend to occur more frequently and thus are more dominant. Among the first 32 harmonics, the fundamental (1st harmonic) appears 6 times, the perfect fifth 4 times, and the major third 3 times, meaning these intervals have a regular frequency of appearance. These are also the main three notes in a major chord.
Next in frequency is a note slightly lower than the minor seventh, which might be surprising, but this is likely related due to the fact that seventh chords are fundamental in blues and similar genres. Additionally, many of the newer appearing notes focus around prime numbers.
Other new harmonics that are not prime numbers include the 9th, 15th, 21st, and 27th harmonics. These can be interpreted as the 3rd harmonic multiplied by 3 (3 × 3 = 9), the 5th harmonic multiplied by 3 (5 × 3 = 15), the 7th harmonic multiplied by 3 (7 × 3 = 21), and the 9th harmonic multiplied by 3 (9 × 3 = 27). In other words, these are related as perfect fifths above already existing harmonics. The perfect fifth interval relative to the fundamental tone has the second highest consonance after the octave and serves as a complementary note that usually isn’t heavily color-coded. This means that the fact that the 3rd harmonic of a specific tone equals the perfect fifth above it signifies a strong relationship. Additionally, the 25th harmonic is related as the 5th harmonic multiplied by 5, which corresponds to a major third, and has the next highest consonance after the perfect fifth. From the perspective of harmonics, prime numbers are clearly special and are directly connected to fundamental principles.

Next time, I will be explaining the relationship between harmonics and chords.

The “sound & person” column is made up of contributions from you.
For details about contributing, click here.