■ The Importance of Timbre
Pitch is important in music, but if the timbre, or tone color is not pleasant, the music cannot truly be enjoyed. For an instrument, if its tone color lacks appeal, no one will want to play it. The role that timbre plays in music is greater than most people may think, and it’s not an exaggeration to say that timbre determines everything in music. Although tone color may seem intangible at first glance, by breaking it down in several ways, its structure begins to reveal itself.

■ The Timbre of an Instrument Is Composed of the Fundamental Tone and Overtones
Even when playing the same C4 (261.6 Hz), each instrument’s timbre differs, allowing us to identify which instrument is playing. The difference in tone color is largely due to the way overtones are produced. If an instrument had no overtones, all sounds would resemble sine waves, and the concept of tone color would disappear. Actual instruments produce sounds above the fundamental tone simultaneously, creating the tone color.
Below is the sound of a piano’s C4 (261.6 Hz), where you can observe peaks at higher frequencies. These peaks are overtones, positioned at integer multiples relative to the fundamental tone. A key point is that the level decreases as the overtone frequency rises. When the sound is composed of such clean, natural overtones, we can perceive pitch. If the overtones deviate significantly from natural overtones, it becomes harder to perceive pitch. Additionally, the piano also produces sounds lower than C4, which are noise components during the attack or sympathetic resonance from other strings. These sounds combine to create the characteristic sound of the piano.
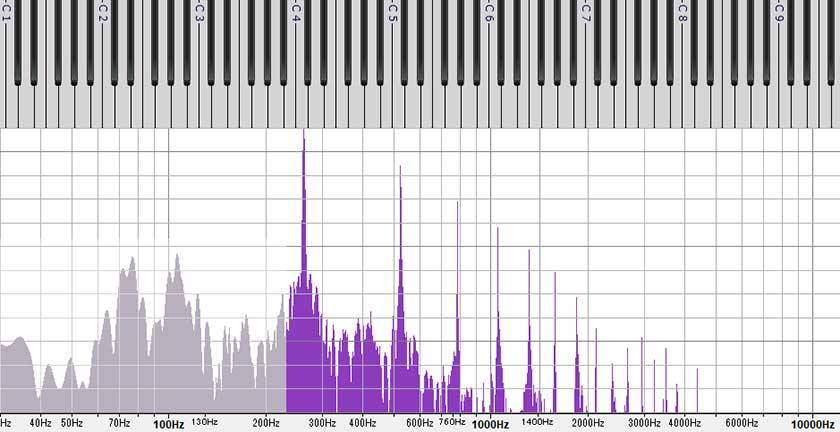
The horizontal axis of the frequency spectrum is logarithmic, which corresponds to the keyboard, as you can see. The logarithmic scale is close to human perception, making it quite convenient. Although it’s hard to see clearly in the diagram, there is a slight difference between natural overtones and equal temperament, so they do not perfectly align with the keyboard.
Next is the example of the high C8 (4186 Hz). The number of overtones is small, with only the slight presence of the octave overtone (2nd harmonic). The gray area below represents noise and resonance sounds. You can see that the lower components are larger than the actual C8 tone being produced.
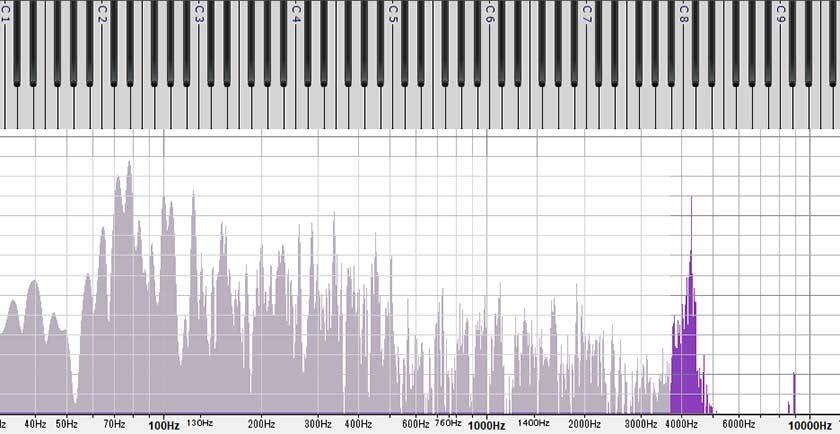
Conversely, the low C2 (65 Hz) has abundant overtones. Generally, the lower the pitch, the more overtones there tend to be. In the case of the piano, when the pitch gets lower, the level of the 2nd harmonic can actually surpass that of the fundamental tone.
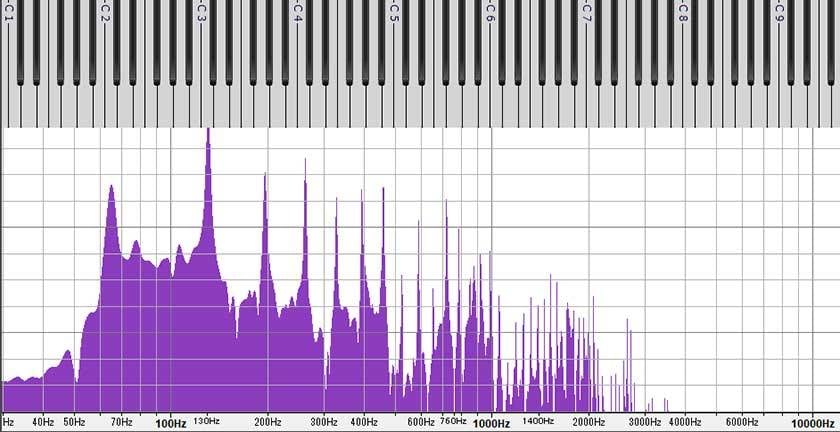
How about the even lower C1 (32.7 Hz)? The level of the fundamental tone is significantly low, and it gives the impression that the sound is really coming from the 2nd harmonic and above. However, the sound feels like a deep bass. When listening, the reason the sound feels low might be more influenced by the overtone structure being an octave lower than the fundamental component. Looking at this frequency spectrum, you can understand that the piano’s low range is pushed quite hard.
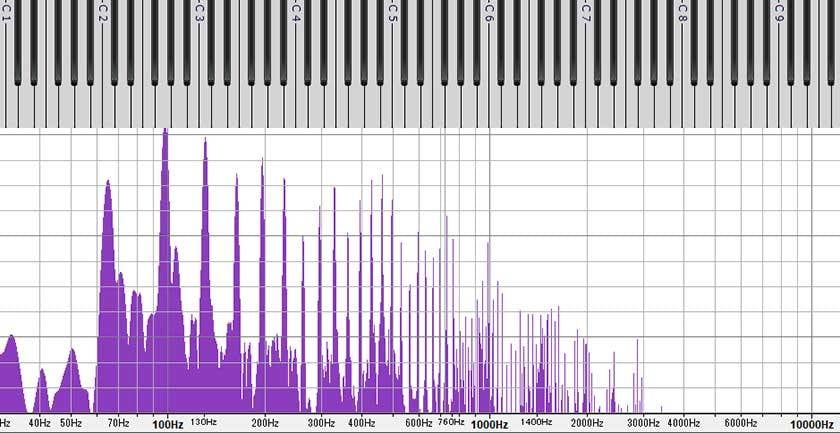
Below is a table showing the overtones up to the 32nd harmonic, taking the fundamental tone as C3. The differences from equal temperament are also listed in cents.
| Harmonic | Interval | Note Name | Difference of Equal Temperament (Cent) |
| Fundamental Tone | Unison | C3 | ±0 |
| 2nd harmonic | 1 octave | C4 | ±0 |
| 3rd harmonic | 1 octave and Perfect 5th | G4 | +1.955 |
| 4th harmonic | 2 octaves | C5 | ±0 |
| 5th harmonic | 2 octaves and Major 3rd | E5 | -13.686 |
| 6th harmonic | 2 octaves and perfect 5th | G5 | +1.955 |
| 7th harmonic | 2 octaves and minor 7th | B♭5 | -31.174 |
| 8th harmonic | 3 octaves | C6 | ±0 |
| 9th harmonic | 3 octaves and Major 2nd | D6 | +3.910 |
| 10th harmonic | 3 octaves and Major 3rd | E6 | -13.686 |
| 11th harmonic | 3 octaves and Aug. 4th | F♯6 | -48.682 |
| 12th harmonic | 3 octaves and perfect 5th | G6 | +1.955 |
| 13th harmonic | 3 octaves and Major 6th | G#6 | +40.528 |
| 14th harmonic | 3 octaves and Minor 7th | B♭6 | -31.174 |
| 15th harmonic | 3 octaves and Major 7th | B6 | -11.731 |
| 16th harmonic | 4 Octaves | C7 | ±0 |
| 17th harmonic | 4 Octaves w/ semitone | C#7 | +4.955 |
| 18th harmonic | 4 Octaves and 1 tone | D7 | +3.91 |
| 19th harmonic | 4 octaves and Minor 3rd | Eb7 | -2.487 |
| 20th harmonic | 4 octaves and Major 3rd | E7 | -13.686 |
| 21st harmonic | 4 octaves w/ Major 3rd + a quarter tone | F7 | -28.909 |
| 22nd harmonic | 4 octaves w/ Perfect 4th | F#7 | -48.389 |
| 23rd harmonic | 4 octaves with Aug. 4th | F#7 | +28.274 |
| 24th harmonic | 4 octaves w/ Perfect 5th | G7 | +1.955 |
| 25th harmonic | 4 octaves and Aug. 5th | G#7 | -27.372 |
| 26th harmonic | 4 octaves with Major 6th | G#7 | +40.267 |
| 27th harmonic | 4 octaves with Major 6th + a quarter tone | A7 | +5.865 |
| 28th harmonic | 4 octaves with minor 7th | A#7 | -31.174 |
| 29th harmonic | 4 octaves with minor 7th + quarter tone | A#7 | +29.345 |
| 30th harmonic | 4 octaves with Major 7th | B7 | -11.731 |
| 31st harmonic | 4 octaves with major 7th + a quarter tone | B7 | +44.817 |
| 32nd harmonic | 5 octaves | C8 | ±0 |
If we compare this to the length of a string and arrange it on a logarithmic piano keyboard, it looks like the following.
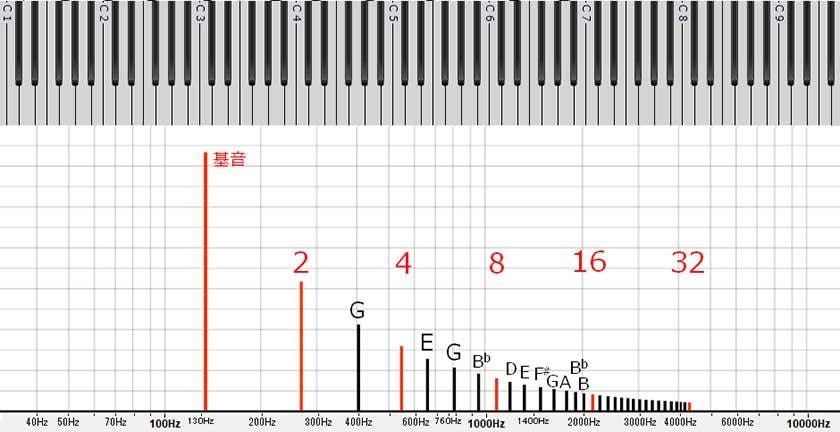
The fundamental tone corresponds to the longest string, and the 2nd harmonic is half that length. Natural harmonics neatly correspond to exact integer fractions. Powers of two (2, 4, 8, 16, 32, ...) represent octaves. The order in which harmonics appear and their pitches contain the fundamental structures of music, such as tuning systems and harmony. Next time, I will explain the tone color brought by the harmonic components.

The column "sound&person" is made possible by submissions from everyone.
For more details on submissions, please see here.
















 DTMセール情報まとめ
DTMセール情報まとめ
 おすすめサイレント楽器特集
おすすめサイレント楽器特集
 ○○やってみた!
○○やってみた!
 みんなでつくる 新・音楽用語事典
みんなでつくる 新・音楽用語事典
 最新コラム&動画をCheck!! OTOYA通信
最新コラム&動画をCheck!! OTOYA通信
 サウンドハウス虎の巻 !
サウンドハウス虎の巻 !