Enchanting Instruments 118 - Harmonics and Chords

When it comes to chords, I would like to take a look from the perspective of the harmonic overtones using a spectrum analyzer.The seven notes of the major scale are arranged here in the order in which they appear as overtones relative to the fundamental.
For the sound source, I’ll be using a straightforward sawtooth wave rich in overtones.
This waveform allows comparison up to high harmonics, making it useful for checking how well the notes blend.
Each of the seven notes is played at the position of its respective overtone.

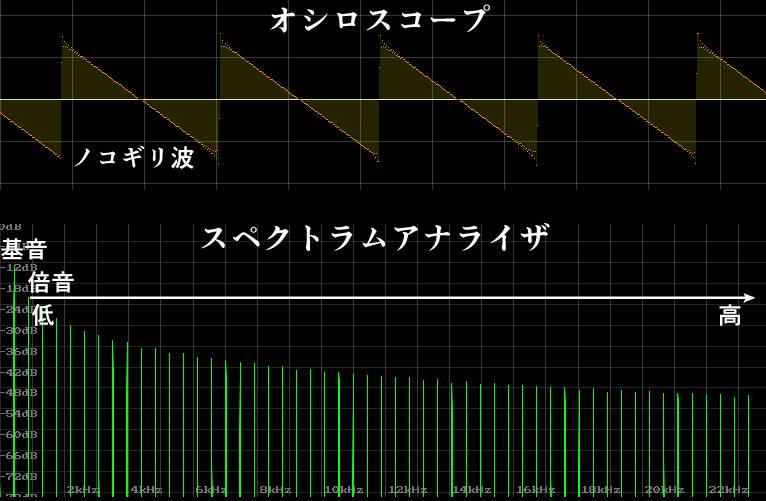
Since the inaccuracies of equal temperament can sometimes become more noticeable, I've also included just intonation when creating the samples.
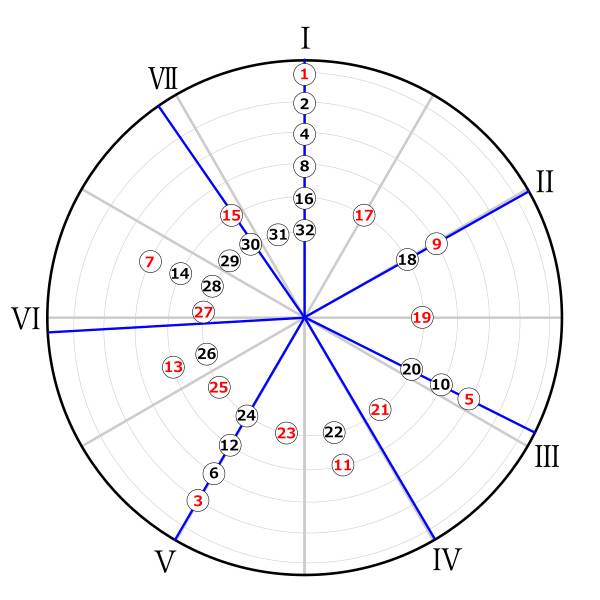
The diagram below shows the layout of the overtones.
The gray, evenly spaced radial lines represent equal temperament, and the blue radial lines represent just intonation.
Harmonics are plotted up to the 32nd overtone.
As you can see, some harmonics stray from both the equal temperament and only the intonation lines. Going further up the harmonic series, more harmonics align with the tuning systems, but the higher the overtone, the less it resonates naturally with the fundamental.
For that reason, two of the notes have been placed in inversion to align with lower harmonics in the samples below.

Octave (2nd Harmonic)

Below is an example where a sawtooth wave at C3 is gradually added to a sawtooth wave at C2.
They are highly compatible, and their harmonics align perfectly with every other overtone.

When you listen to it, the newly added higher octave sound blends completely into the harmonic structure, so it’s barely noticeable as it fades in.
In the latter half, the sound is toggled on and off to make the difference clearer.
An octave interval blends so well that it hardly gives the impression of a chord.
As a measure of how well two notes blend, you can check what percentage of the fundamental's harmonics change in level.
In the case of an octave, every other harmonic aligns, so I’ll say it's about 50%.

Perfect Fifth (3rd Harmonic)

The perfect fifth corresponds to the 3rd harmonic, so the third bar from the left represents the fundamental.
Its harmonics also align neatly.
One of its characteristics is that it supplements the fundamental without adding much color.
The perfect fifth is the most harmonically compatible interval after the octave.
Even in equal temperament, the discrepancy is within an acceptable range.
Blending rate: 33%.

Major Third (5th Harmonic)

The major third corresponds to the 5th harmonic, so the fifth bar from the left represents the fundamental, making it an important tone in forming a major chord.
Since this is created using just intonation, you can see it aligns neatly with the root’s harmonics.
In equal temperament, the dissonance caused by tuning discrepancies becomes more noticeable, but if the harmonic content is low or the sustain is short, it’s not too problematic.
Blending rate: 20%.

Major Second (9th Harmonic)

The major second, or 9th harmonic, is easy to handle as it has very little deviation in both just intonation and equal temperament.
From another perspective, it can be seen as a perfect fifth above the 3rd harmonic.
In practical use, it’s a key note in ninth chords.
While it may seem complex in music theory as a tension note, from a harmonic standpoint, it’s a highly compatible and easy-to-use tone.
Blending rate: 11%.

Major Seventh (15th Harmonic)

With just intonation, it fits nicely within the harmonic spectrum.
However, since it is a double-digit harmonic and far from the fundamental, it inevitably feels somewhat detached.
The blending rate is 6.7%.
When the blending rate falls below 10%, the tone tends not to feel well-integrated.
Lower-order harmonics blend more naturally due to their stronger connection with the fundamental, so the 15th harmonic occupies a somewhat delicate position.

Major Sixth as 19th Harmonic in Inversion

The major sixth has a large discrepancy in just intonation, and even in equal temperament, there’s a slight mismatch, making it difficult to use.
Moreover, since it’s the 27th harmonic, it's quite distant from the fundamental, and the blending rate drops to 3.7%, making it prone to sounding detached.
To address this, we’ll use its inverted form.
By placing the major sixth below the fundamental, the fundamental is treated like a minor third from the 19th harmonic.
Even so, the blending rate is still as low as 5.3%.
This corresponds to the parallel minor key.
Minor keys tend to present theoretical complications.
If you want to treat it as a lower-order harmonic, you could think of it as a perfect fifth above the 9th harmonic.
In other words, it's not a tone directly tied to the fundamental, but rather one that pairs well with the major second.
If prioritizing blending, ideally, the harmonic number should remain in single digits.

Perfect Fourth as Inverted 3rd Harmonic

If we consider the perfect fourth as the 21st harmonic, it has discrepancies in both just intonation and equal temperament, making it a difficult interval to harmonize.
There is also the idea of using even higher-order harmonics, but the blending rate drops off significantly as the harmonic number increases.
Fundamentally, the concept of dividing the octave into 12 tones is based on the perfect fifth, which adds to the complexity.
Therefore, this interval is also treated in its inverted form.
By placing the perfect fourth below the fundamental, the fundamental is treated as a perfect fifth above the 3rd harmonic.

To Summarize

Most notes align with the harmonics of the fundamental sawtooth wave.
In other words, the harmonic structure remains entirely unchanged from the fundamental sawtooth wave, with only a partial shift in harmonic levels.
When there’s no deviation in the harmonics, the sound is completely harmonious and free of dissonance.
In the actual chords, however, tones are often constructed within one octave as closed voicings, and in equal temperament, the fundamental and harmonics don’t always match up, making the kind of harmony described above difficult to achieve.
Even so, knowing the relationship of harmonics as explained above is incredibly useful.
In particular, the placement of the bass allows you to control the overall stability of the sound.
Looking at the above, you can imagine that the richer the bass harmonics are, the more the entire sound is enveloped.
Even though the bass is monophonic, its rich harmonics influence the full range of frequencies.
Finally, let’s try an experiment by adding harmonics at random.
All notes are still contained within a single sawtooth wave.

In the next article, we’ll explore major and minor chords from a harmonic perspective.
Major chords are generally said to sound bright, while minor chords are said to sound sad.
However, we’re going to explore whether that can actually be said to be true in harmonics.

The “sound & person” column is made up of contributions from you.
For details about contributing, click here.