Enchanting Instruments 79 - Loudness Meter 3

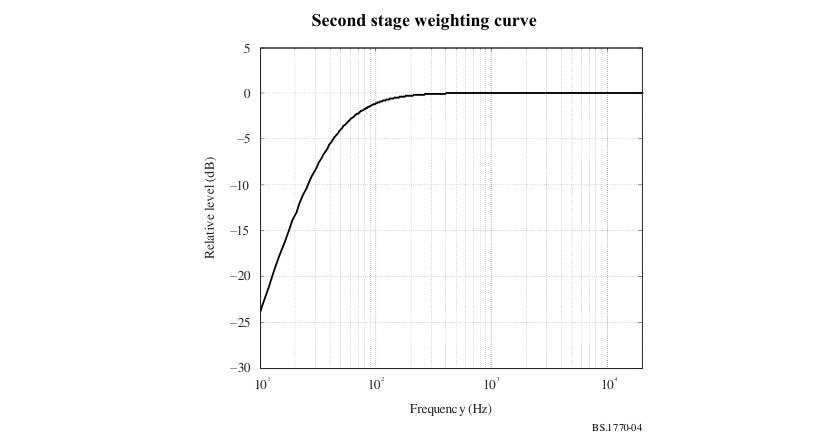
A Close-up at the K-filter

The K-filter is realized by connecting a high shelf and a high pass filter (B characteristic curve) in order; K is not an abbreviation, but it’s an international standard, which is determined as A, B, and C in that order. It’s named K because of its flow.

The ITU document carefully and concretely proposes a second-order IIR (infinite impulse response) digital filter, which is mathematically intractable because it is a digital emulation of an analog circuit, but it is not so troublesome to use. The IIR filter shown in the ITU document is for a sampling frequency of 48,000 Hz, but coefficients are available, so a K-filter can be easily created and tested.

The first filter is high-shelf, which elevates the high frequencies.

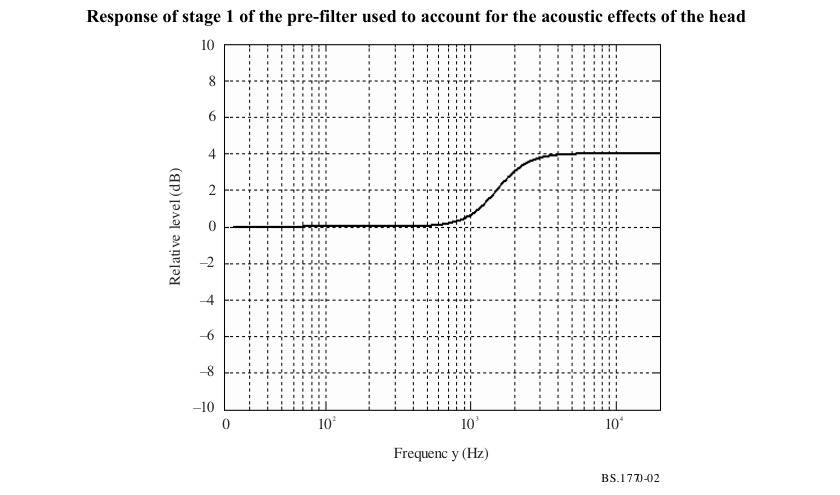
Block diagram. The 2nd order filter in the 2nd line corresponds to Z in the figure. The figure shows the number of delay taps. The table shows the coefficients. By changing these coefficients, the filter can be transformed into various types of filters. This K-filter also realizes two types of filters, high-shelf and high-pass, by simply changing the coefficients.

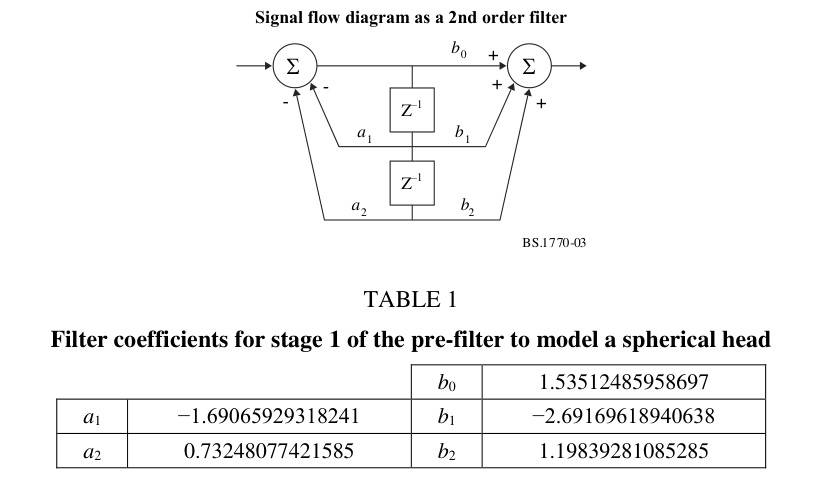
Since I went through the trouble, I tried to quickly build it with Audacity, a waveform editing software. The programming source is as follows.

;control b0 "b0" real " " 1.5351248958697 -3.0000 3.0000
;control b1 "b1" real " " -2.69169618940638 -3.0000 3.0000
;control b2 "b2" real " " 1.19839281085285 -3.0000 3.0000
;control a0 "a0" real " " 1.0 -3.0000 3.0000
;control a1 "a1" real " " -1.69065929318241 -3.0000 3.0000
;control a2 "a2" real " " 0.73248077421585 -3.0000 3.0000
(biquad-m s b0 b1 b2 a0 a1 a2)

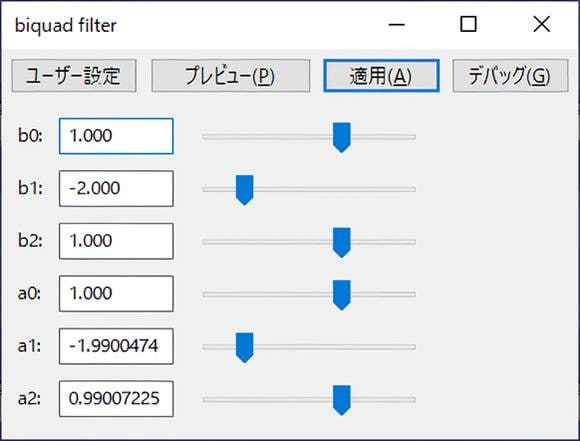
When executed, the interface is as follows.

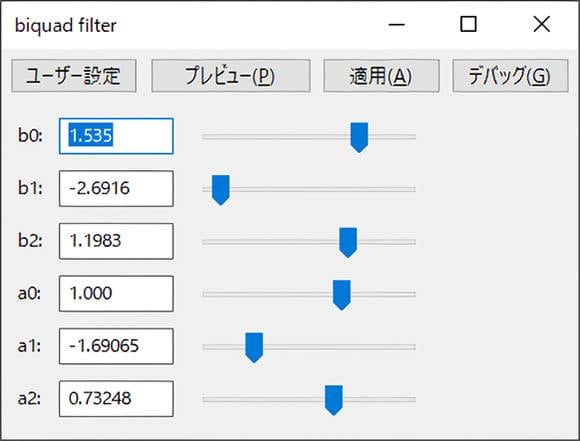
When applied to white noise, you can see that the frequency above 3 kHz is raised by about 4 dB.

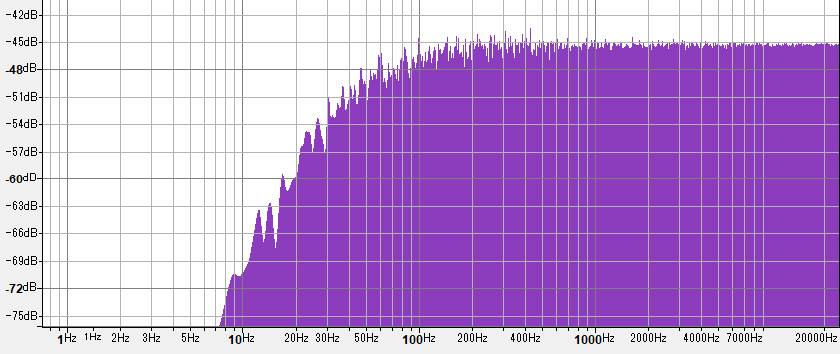
In the same way, try a high-pass filter (B characteristic curve). This filter cuts the low frequency range.

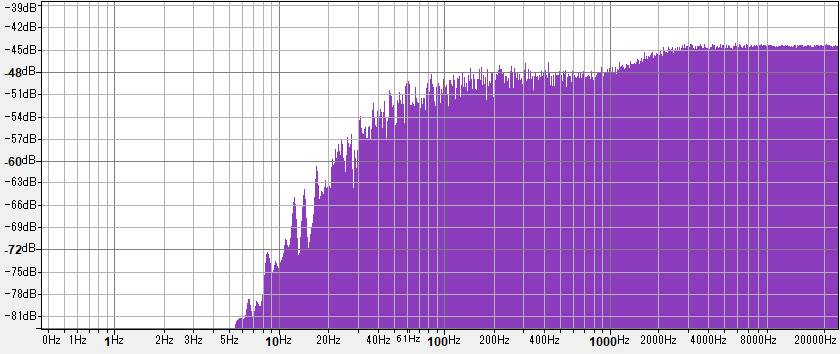
This also applies to white noise. It works properly.

When the above high shelf and high pass filter are connected in series, the K-filter is completed as shown below.

RMS (Root Mean Square)

First, RMS value (Root Mean Square) = Root Mean Square = RMS value. This means that we are looking at power, not peaks; Momentary (400ms), Short-term (3s), and Integrated (all) are basically the same, even though they handle different times.

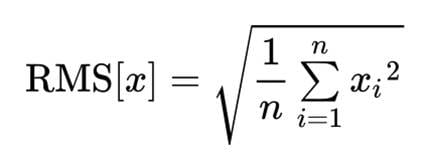
The contents of the above formula are Root(Mean(Square(x))), as the name RMS implies. However, the order of calculation is reversed since it is done from the inside of the parentheses.

1. Square -Find the square of each data and sum of the whole range.
2. Mean - Divide by the number of data to get the mean of the squares.
3. Root - square root of the mean value gets you the RMS value.

Let’s look at the case of a simple sine wave. For one cycle of amplitude plus or minus one, squaring gives a red waveform. Since the average of this will be 0.5, its Root will be sqrt(0.5)=0.707, so RMS will be 0.707.

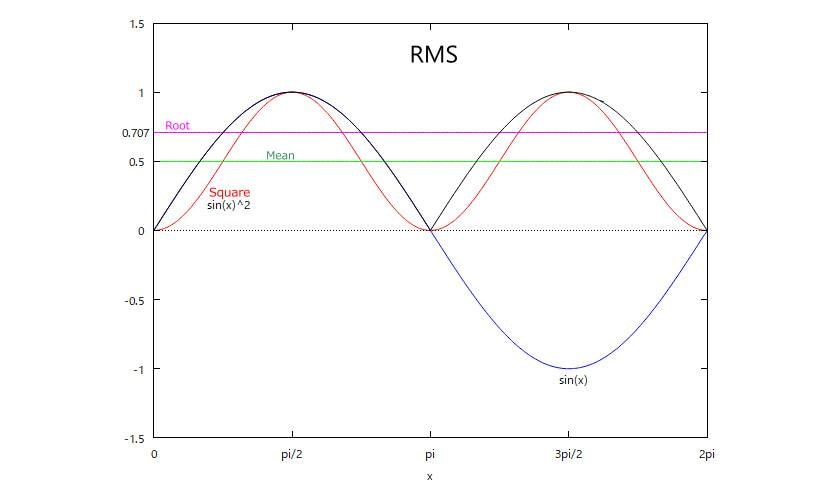
Weight Factor G

The weight coefficient compensates for the angle of incidence of sound. The loudness meter assumes surround sound, so GL Left (1.0), GR Right (1.0), GC Center (1.0), GLS Left Surround (1.41), and GRS Right Surround (1.41) are used. For music that only deals with stereo material, they are all 1.0, which is the same as nothing.

Safety Gate

This was not available in 2006; it was included in 2011. Since human perception tends to be dominated by loudness, it became clear that if silent or relatively quiet sound sections are processed in the same way, they will not be as loud as how people perceive them to be. By employing a gate that excludes quiet intervals, a more consistent loudness value can be obtained. There are two types of gates used by loudness meters.

Absolute gate

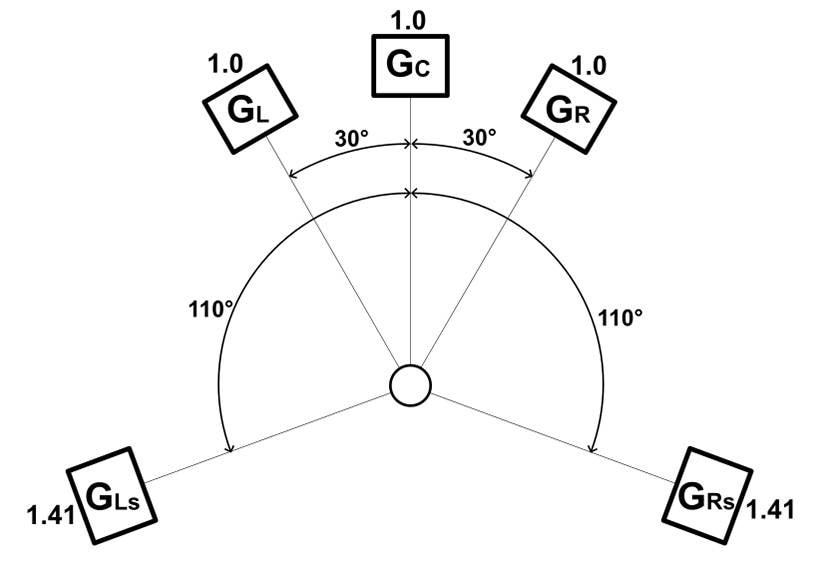
-70 LUFS treats anything less than 70 LUFS as silence, which is eliminated in LUFS-I. The figure below shows white noise for 60 seconds, with -4.6 LUFS for the first 30 seconds and less than -70 LUFS for the second half. Visually, it appears to be silent, but there is a small sound. In this case, the absolute gate is activated and the portion considered silent is not counted. As a result, LUFS-I outputs -4.6 LUFS. This is the absolute gate.

Relative Value Gate

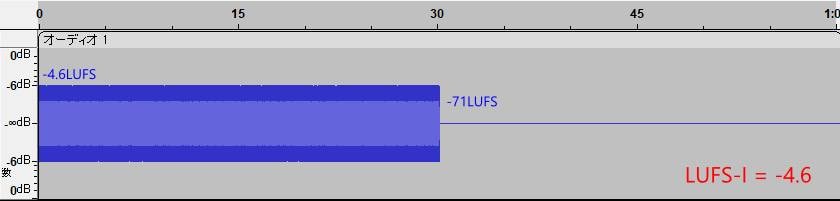
Removes less than -10 LU(dB) than the average of signals passing through the absolute gate. The figure below shows a 60-second white noise with -4.6 LUFS for the first 30 seconds and -12 LUFS lower than -16.6 LUFS for the second half. LUFS-I results in -7.4 LUFS. From these figures, we can see that the relative-value gate was released in the middle of the process.

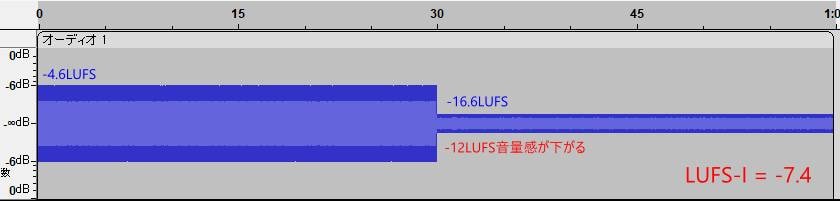
If I use Reaper to monitor the movement of LUFS-I, we can see that the relative value gate remains in place for about 20 seconds after it is turned on, but then it deactivates and the -12 LUFS low signal is reflected in the LUFS-I.

In the next issue, we will look at the specific behavior of the combination of the two.

The “sound & person” column is made up of contributions from you.
For details about contributing, click here.